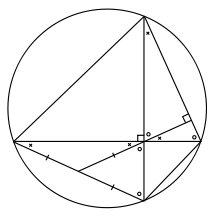
Exploring geogebra#1 PENTOMINOES IN GEOGEBRA#3 Euclid's Midpoint Theorem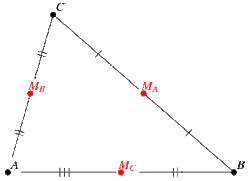
A direct proof of ONE of Eulcid's midpoint theorems.
#5 Pythagorean theorem proof(s)#6 Tessellation#8 Roman Numerals#10 2nd Book Skimpression
I think for a lot of people having to get anywhere near e in mathematics (and fuel) is a bit scary. Not only that, it can be a little complicated. What I found while skimming over the book The Story of e is that the the number e is more fascinating than it is scary. Not only that it has been around longer than one would think. Even before calculus! Without even realizing it people encounter the number e more often outside of a classroom than they do inside one. Overall, simply based on a skim read, I would recommend the book as a "should read". I would suggest it even more for anyone who can't quite grasp the concept of the number e or anyone who asks the age old question, "why do I need to know this"?
#12 Women in mathematics: Emmy Noether
Usually when we hear about women in mathematics it's in reference to "newer" mathematicians, but when I stumbled across Emmy Noether's biography I have to say I was more than impressed. Now I my self am not at all good with abstract algebra, but what this woman has done is phenomenal! You know it's the real deal when Albert Einstein gives you praises! Not only did Emmy revolutionize the theories of rings, fields, and algebra, she also overcame many, many social barriers. Below I have links to some websites that detail the life and work of mathematician Emmy Noether.
Wikipedia Smithsonian Emmy #13 Exploring Infinity (Blog and Daily Work)
In my blog I explored infinty and looked into a few fun facts. Check it out here!
|
#2 Brahmagupta's Theorem (Making sense of it)Brahmagupta's Theorem. If an inscribed quadrilateral's diagonals intersect at a right angle, then the perpendicular to a side from the point of intersection of the diagonals always bisect the opposite side.
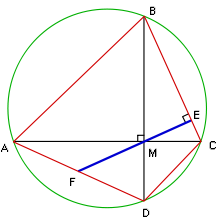
So, as I begin my search to decipher what Brahmaggupta's Theorem set out to prove and to put it in modern language, I stumble upon tons of images like the one to the left. After reading the numerous versions of the theorem I figured out the proof of the theorem simply proves that (using the figure to the left) if we are given four points on a circle A, B, C, and D such that AC is perpendicular to BD and intersect at a point M, and we drop the perpendicular from the point M to the lines BC and AD to construct the points E and F at the intersections, then F is the midpoint of the line AD.
#4 Proofs of Brahmagupta's theorem(s)#7 Qualitative Graphs#9 Sudoku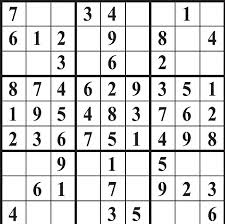
Sudoku is another math game (or activity) that is a great way to relieve stress and it is similar to Magic Squares! For my daily work I spent some time trying out Sudoku puzzles at different levels of difficulty.
#11 6 Numbers! (A Game of Algebra)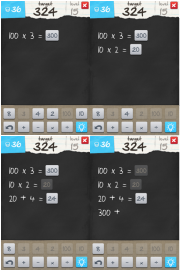
For this particular daily work I decided to play a game called 6 Numbers. In this game one uses the operations addition, subtraction, division, and multiplication with 6 numbers to ultimately reach a target number. The catch is each number can only be used once and the only other numbers that can be used are the ones created using the 6 originals.
|
||||||